- Au voisinage de 0: On sait que
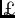 , donc
, donc
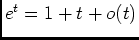 intégrable au voisinage de 0.
intégrable au voisinage de 0.
Au voisinage de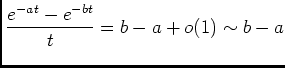 : On sait que
: On sait que
 , donc
, donc
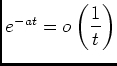 intégrable au voisinage de
intégrable au voisinage de 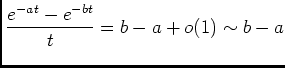 .
.
-
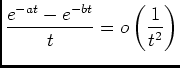 , trés evident.
, trés evident.
Posons: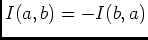 , donc:
, donc:
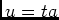 .
.
- L'application:
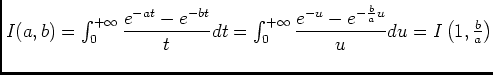 est continue sur
est continue sur
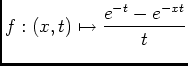 en tant que somme, rapport de fonctions continue, qui ne s'annule pas. En
en tant que somme, rapport de fonctions continue, qui ne s'annule pas. En  on a:
on a:
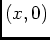 continue, donc
continue, donc 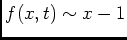 est continue sur
est continue sur
 .
.
D'autre part: pour![$ x\in[a,b]\subset[1,+\infty[$](img16.png) on a:
on a:
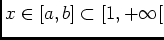 qui est continue, intégrable sur
qui est continue, intégrable sur
![$ ]0,+\infty[$](img18.png) , donc
, donc 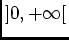 est continue sur
est continue sur
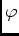 .
.
- Pour
![$ x\in[a,b]\subset[1,+\infty[$](img16.png) on a:
on a:
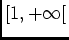 continue, intégrable sur
continue, intégrable sur
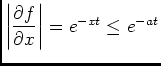 . Donc
. Donc 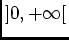 est de classe
est de classe
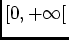 sur
sur
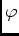 , avec
, avec
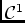 .
.
- D'aés le raisonnement fait dans la question précédente, on a:
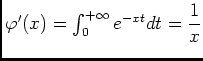 , donc
, donc
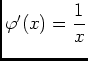 , or
, or
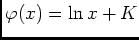 , d'où
, d'où 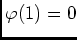 et donc
et donc
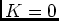 .
.
- L'application:
- Si
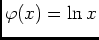 , alors
, alors
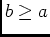 , donc
, donc
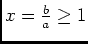 .
.
Si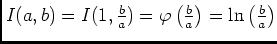 , alors
, alors
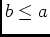 , donc:
, donc:
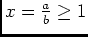 .
.
Conclusion: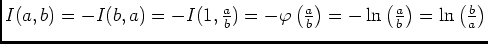 .
.
- Au voisinage de 0: on sait que
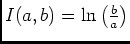 , d'où
, d'où
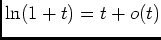 intégrable au voisinage de 0, donc
intégrable au voisinage de 0, donc
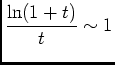 est intégrable sur
est intégrable sur ![$ ]0,1]$](img40.png) .
.
- Posons
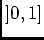 , on a
, on a
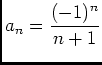 , donc le rayon de convergence de la série
, donc le rayon de convergence de la série
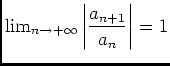 est égal à 1, dont la somme est
est égal à 1, dont la somme est
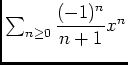 , puisqu'il s'agit de son développement en série entière.
, puisqu'il s'agit de son développement en série entière.
- Pour
![$ x\in [0,1]$](img45.png) fixé, on vérifie faciulement que la série
fixé, on vérifie faciulement que la série
 est une série alternée, donc vérifie le critère spécial, en prticulier la majoration du reste par son 1ér terme, donc
est une série alternée, donc vérifie le critère spécial, en prticulier la majoration du reste par son 1ér terme, donc
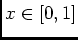 , donc le reste converge uniformément vers 0, et par suite la convergence de la série sur
, donc le reste converge uniformément vers 0, et par suite la convergence de la série sur ![$ [0,1]$](img47.png) est uniforme.
est uniforme.
-
![\begin{displaymath}\begin{array}[t]{ll}
\ds\int_0^1\dfrac{\ln(1+t)}{t}dt&=\ds\i...
...}^{+\infty}\dfrac{1}{p^2}\\
&=\dfrac{\pi^2}{12}
\end{array}\end{displaymath}](img48.png)
 est de classe
est de classe
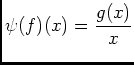 , donc
, donc 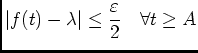 on a:
on a:
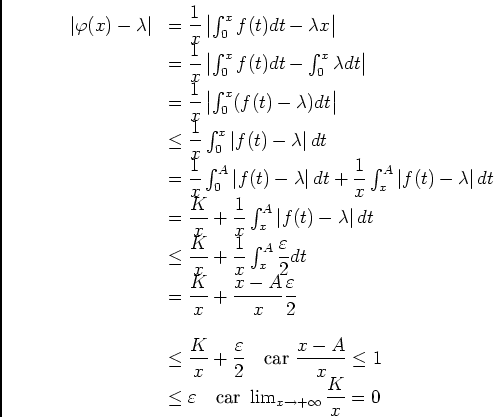 , on a:
, on a:
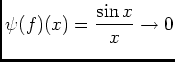 , alors que
, alors que
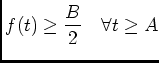
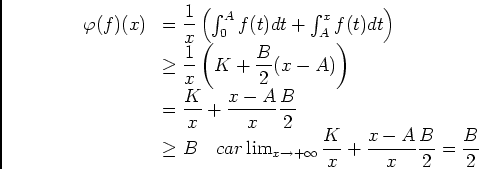 .
.
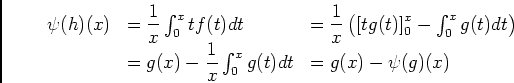 admet une limite finie en
admet une limite finie en 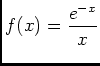 , alors que
, alors que
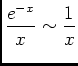 , quand
, quand
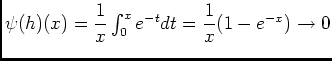 et
et 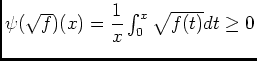 , on aura:
, on aura:
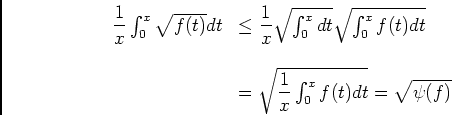 , n'oubliez pas de le mentionner pour
, n'oubliez pas de le mentionner pour 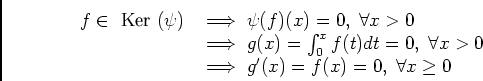 est un exemple de fonction de
est un exemple de fonction de  non nulle telle que
non nulle telle que
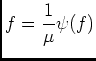 d'aprés 4.1). De plus d'aprés 1.1) on peut affirmer que
d'aprés 4.1). De plus d'aprés 1.1) on peut affirmer que 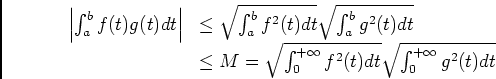 est intégrable sur
est intégrable sur
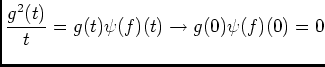 , car
, car 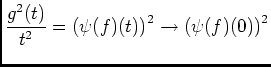 est intégrable sur
est intégrable sur ![$ ]0,b]$](img128.png) car prolongeable par continuité en
car prolongeable par continuité en 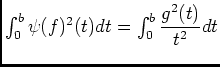 , donc
, donc
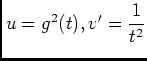 et
et
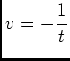
![\begin{displaymath}\begin{array}[t]{ll}
\ds\int_0^b\psi(f)^2(t)dt&\ioe 2\ds\int...
...\quad\text{D'aprés l'inégalité de Cauchy-Shwarz. }
\end{array}\end{displaymath}](img135.png) ,
,
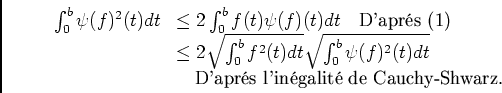 , c'est terminé, sinon on peut simplifier avec et on obtient encore le résultat demandé.
, c'est terminé, sinon on peut simplifier avec et on obtient encore le résultat demandé.
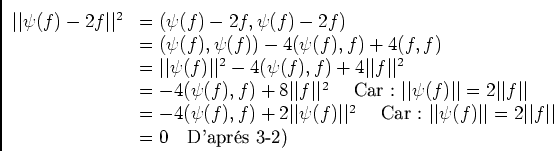 , ainsi si
, ainsi si 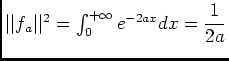 .
.
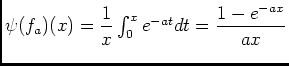 .
.
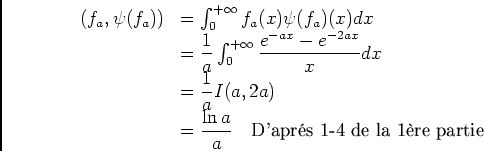 .
.
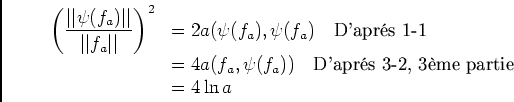 .
.
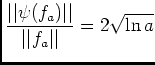 .
.
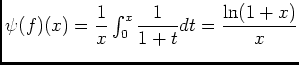 .
.
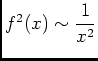 .
.
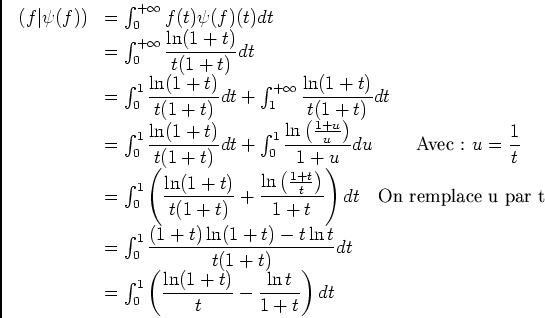 , donc
, donc
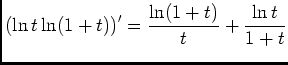 est une primitive de
est une primitive de
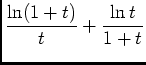 et
et
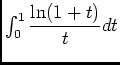 , en effet:
, en effet:
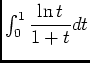
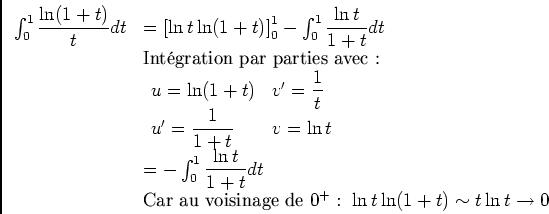 et
et
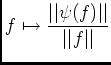 est un connexe dans
est un connexe dans
 en tant qu'image d'un connexe par une application continue, d'autre part:
en tant qu'image d'un connexe par une application continue, d'autre part:
![$ ]0,2[$](img167.png) .
.
![$ [0,a+1]$](img169.png) , avec:
, avec:
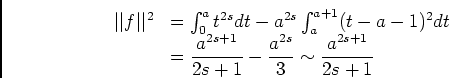 , on a:
, on a:
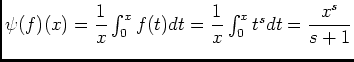 .
.
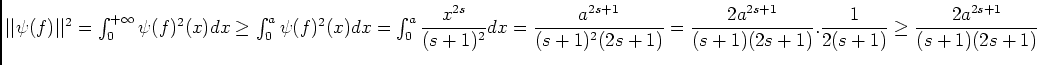 .
.
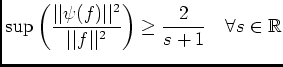 , donc pour
, donc pour
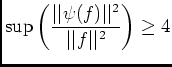 , or d'aprés la question 4.2) on a:
, or d'aprés la question 4.2) on a:
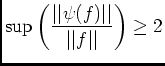 , d'où l'égalité.
, d'où l'égalité.
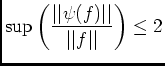 est bien intégrable car
est bien intégrable car
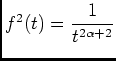 , avec:
, avec:
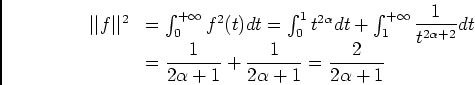 pour
pour 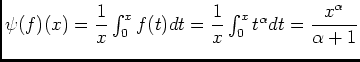 , alors:
, alors:
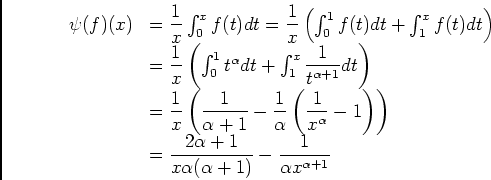
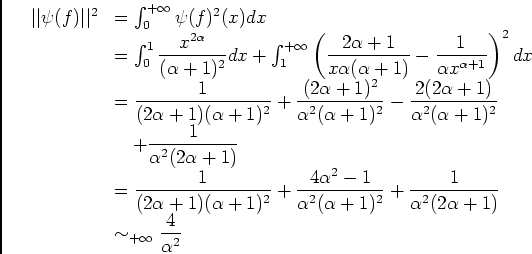 pour
pour 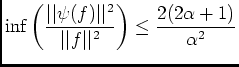 assez grand, quand
assez grand, quand
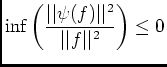 , d'où l'égalité.
, d'où l'égalité.