


suivant: À propos de ce
| Concours commun national marocain 2005: |
| corrigé epreuve Math 1, MP |
|---|
I. Résultats préliminaires.
A- Un résultat de dérivation.
- La formule de Taylor-Young à l'ordre 2, s'écrit:
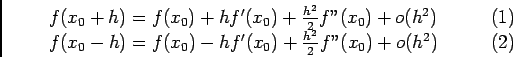
- En faisant (1)+(2), on obtient:
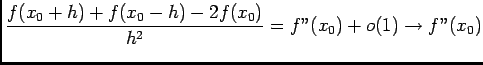 , quand
, quand
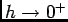 .
.
- Si
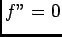 , on peut affirmer que
, on peut affirmer que 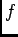 est affine.
est affine.
A- Un résultat de convergence.
- ?
-
![\begin{displaymath}\begin{array}{ll}
\\ ds\int_0^{2\pi}b_n^2\sin^2(nx)dx&=\dfr...
...n(2nx)}{2n}\right]_{x=0}^{x=2\pi}\\
&=\pi b_n^2
\end{array}\end{displaymath}](img7.png) .
.
Ainsi
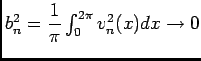 , quand
, quand
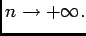
-
 , d'où
, d'où
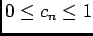 , donc
, donc 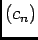 est bornée.
est bornée.
D'autre part
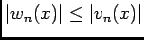 , et
, et
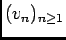 converge simplement vers 0, donc
converge simplement vers 0, donc
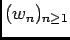 aussi.
aussi.
- Ainsi
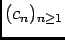 est bornée et
est bornée et
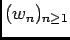 converge simplement vers 0, en faisant jouer à
converge simplement vers 0, en faisant jouer à 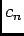 le rôle joué par
le rôle joué par 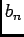 dans la question précédente, on déduit que
dans la question précédente, on déduit que
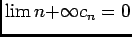 , donc à partir d'un certain rang
, donc à partir d'un certain rang 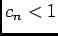 , pour cela utilier la définition de la limite pour
, pour cela utilier la définition de la limite pour 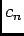 avec
avec
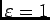 , et alors
, et alors 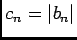 à partir d'un certain rang, donc
à partir d'un certain rang, donc
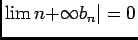 et par suite
et par suite
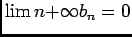 .
.
II. Série trigonométrique dont la somme est continue.
- Pour tout réel,
 , la série numérique
, la série numérique
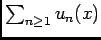 est convergent, donc son terme génbéral
est convergent, donc son terme génbéral 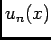 converge vers 0.
converge vers 0.
- En particulier
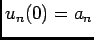 converge vers 0.
converge vers 0.
-
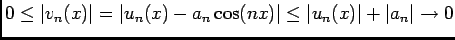 , quand
, quand
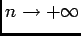 , donc
, donc
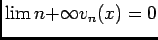 , pour tout réel,
, pour tout réel,  . Ainsi
. Ainsi 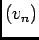 converge simplement vers 0, et d'aprés la partie I.B, on peut conclure que
converge simplement vers 0, et d'aprés la partie I.B, on peut conclure que
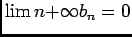 .
.
-
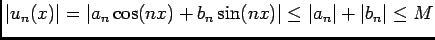 , car
, car
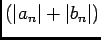 est bornée, puisqu'elle converge vers 0, ainsi
est bornée, puisqu'elle converge vers 0, ainsi
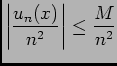 et d'autre part
et d'autre part
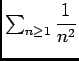 est une série de Riemann convergente, donc
est une série de Riemann convergente, donc
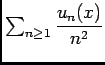 converge normalement, dont le terme général est continue donc sa somme est aussi continue.
converge normalement, dont le terme général est continue donc sa somme est aussi continue.
- Pour tout réel,
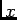 et tout entier,
et tout entier, 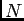 , on a
, on a
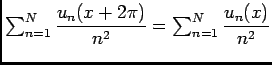 , quand on fait tendre
, quand on fait tendre 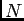 vers
vers 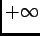 , on obtient
, on obtient
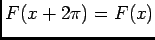 , donc
, donc 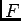 est
est 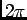 -périodique.
-périodique.
Calculons les coéfficients de Fourrier de 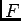
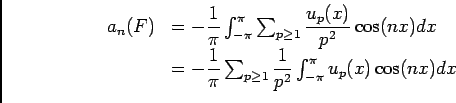
On peut permuter signes somme et intégrale vu qu'il y a convergence normale sur
![$ [-\pi,\pi]$](img45.png) .
.
D'autre part:
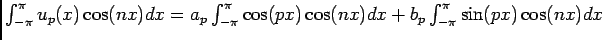 Et on sait que:
Et on sait que:
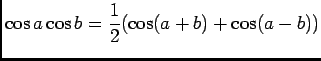 , donc
, donc
![$ \ds\int_{-\pi}^\pi\cos(px)\cos(nx)dx=\dfrac 12\ds\int_{-\pi}^\pi(\cos (n+p)x+\...
...eft[\dfrac{\sin (n+p)x}{n+p}+\dfrac{\sin (n-p)x}{n-p}\right]_{x=-\pi}^{x=\pi}=0$](img48.png) si
si 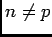
Si 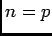 , alors
, alors
![$ \ds\int_{-\pi}^\pi\cos(px)\cos(nx)dx=\ds\int_{-\pi}^\pi\cos^2(nx)dx=\dfrac 12\...
...+p)x+1)dx=\dfrac 12\left[\dfrac{\sin (n+p)x}{n+p}+x\right]_{x=-\pi}^{x=\pi}=\pi$](img51.png) .
.
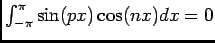 car il s'agit d'intégrer sur
car il s'agit d'intégrer sur
![$ [-\pi,\pi]$](img45.png) une fonction impaire.
une fonction impaire.
Conclusion:
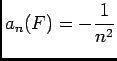 . Et pareil pour le calcul de
. Et pareil pour le calcul de 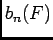 .
.
- On a
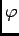 est continue sur
est continue sur
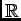 et de classe
et de classe
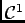 sur
sur
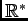 , avec
, avec
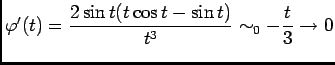 quand
quand
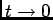 , donc
, donc 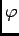 est de classe
est de classe
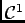 sur
sur
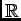
-
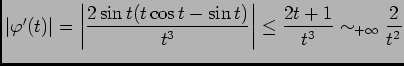 , intégrable au voisinage de
, intégrable au voisinage de 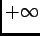 , donc
, donc 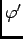 aussi.
aussi.
-
![\begin{displaymath}\begin{array}[t]{l}
\dfrac{F(x+2h)+F(x-2h)-2F(x)}{4h^2}\\ ...
...}^{+\infty}(a_n\cos (nx)+b_n\sin (nx))\varphi (nh)
\end{array}\end{displaymath}](img63.png)
- Commençons par le 2 ème membre de l'égalité:
![\begin{displaymath}\begin{array}[t]{l}
\ds\sum_{n=0}^{+\infty}\left(S_n(x)-f(x)...
...nx)\\
=\dfrac{F(x+2h)+F(x-2h)-2F(x)}{4h^2}-f(x)
\end{array}\end{displaymath}](img64.png)
- Découle de la définition de la limite:
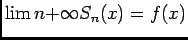 pour
pour 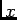 , fixé.
, fixé.
- On a:
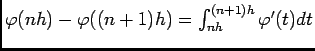 , donc
, donc
![\begin{displaymath}\begin{array}[t]{l}
\left\vert\ds\sum_{n=N}^{+\infty}\left(S...
...0}^{+\infty}\left\vert\varphi '(t)\right\vert dt=A
\end{array}\end{displaymath}](img67.png)
- D'aprés la question précédente, on peut conclure que
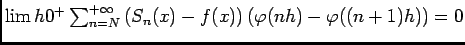 , d'autre part
, d'autre part
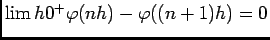 pour tout
pour tout
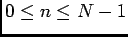 , donc
, donc
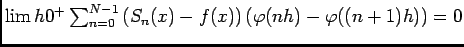 , puisqu'il s'agit d'une somme finie, et par suite
, puisqu'il s'agit d'une somme finie, et par suite
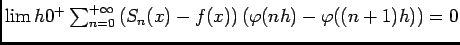 , donc tenant comte de la question 4.2, on peut conclure que
, donc tenant comte de la question 4.2, on peut conclure que
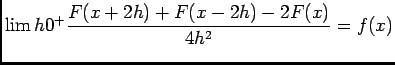
- Dans cette question il semble y avoir une erreur d'énoncé, il fallait plutôt montrer que
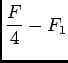 est affine au lieu de
est affine au lieu de 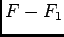
Posons
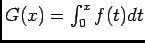 , et utilisons une intégration par partie dans
, et utilisons une intégration par partie dans 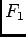 où
où
![\begin{displaymath}\begin{array}[t]{ll}
u'(t)=f(t)&\quad u=G(t)\\
v(t)=x-t&\quad v'(t)=-1
\end{array}
\end{displaymath}](img78.png) , alors
, alors
![$ F_1(x)=\left[(x-t)G(t)\right]_{t=0}^{t=x}+G(t)=\ds\int_0^xG(t)dt$](img79.png) est de classe
est de classe
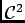 car
car 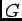 est de classe
est de classe
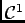 l'est en tant que primitive d'une fonction continue, avec
l'est en tant que primitive d'une fonction continue, avec 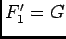 et
et 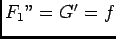 .
.
- D'aprés le préliminaire
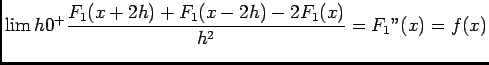 , on pose
, on pose
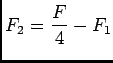 , alors:
, alors:
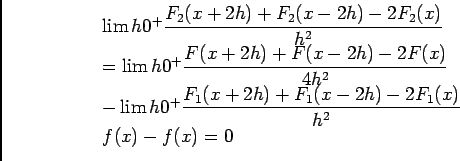
, donc
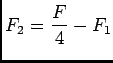 est affine et par suite
est affine et par suite 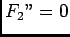 , d'où
, d'où
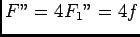 .
.
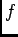 est
est 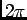 -périodique en tant que limite simple de fonctions
-périodique en tant que limite simple de fonctions 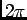 -périodique.
-périodique.
Calculons les coéfficients de Fourier associés à 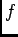 .
.

Or
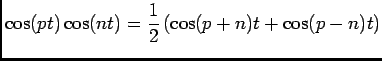 , donc:
, donc:
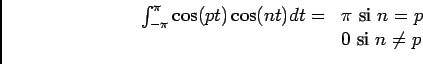
et
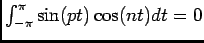 , comme integrale sur
, comme integrale sur
![$ [-\pi,\pi]$](img45.png) d'une fonction impaire.
d'une fonction impaire.
Donc
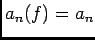 et de même on montre que
et de même on montre que
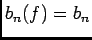 .
.
III. Séries trigonométriques impaires.
A- Une application à l'étude précédente.
- Pour tout réel,
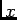 fixé on a
fixé on a
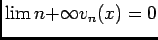 , en tant que terme général d'une série numérique convergente, et d'aprés la partie I.B on peut affirmer que
, en tant que terme général d'une série numérique convergente, et d'aprés la partie I.B on peut affirmer que
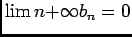 .
.
- La suite
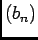 est bornée par un réel
est bornée par un réel 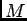 , car convergente, donc
, car convergente, donc
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v_n(x)}{n^2(n^2+1)}\ri...
...oe \dfrac{M}{n^2(n^2+1)}\\
&\ioe \dfrac{M}{n^4}
\end{array}\end{displaymath}](img97.png) et
et
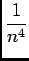 est le terme général d'une série de Rieman convergente, donc
est le terme général d'une série de Rieman convergente, donc
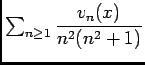 converge normalement sur
converge normalement sur
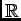 . D'autre part:
. D'autre part:
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v'_n(x)}{n^2(n^2+1)}\r...
...\ioe \dfrac{M}{n(n^2+1)}\\
&\ioe \dfrac{M}{n^3}
\end{array}\end{displaymath}](img100.png) et
et
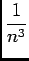 est le terme général d'une série de Rieman convergente, donc
est le terme général d'une série de Rieman convergente, donc
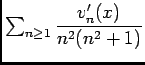 converge normalement sur
converge normalement sur
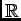 , et enfin
, et enfin
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v''_n(x)}{n^2(n^2+1)}\...
...&\ioe \dfrac{M}{(n^2+1)}\\
&\ioe \dfrac{M}{n^2}
\end{array}\end{displaymath}](img103.png) et
et
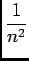 est le terme général d'une série de Rieman convergente, donc
est le terme général d'une série de Rieman convergente, donc
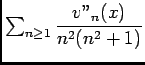 converge normalement sur
converge normalement sur
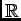 . Et ainsi on peut dériver sous le signe somme, d'où
. Et ainsi on peut dériver sous le signe somme, d'où 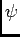 est de classe
est de classe
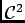 , avec:
, avec:
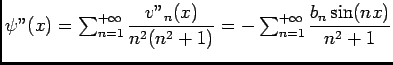 .
.
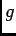 est bien définie car elle converge normalement d'aprés la question précédente, d'autre part
est bien définie car elle converge normalement d'aprés la question précédente, d'autre part
 converge simplement et continue, donc
converge simplement et continue, donc
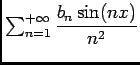 est de classe
est de classe
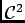 , et aussi
, et aussi
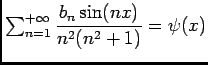 , avec la possibilité de dériver sous le signe somme, donc
, avec la possibilité de dériver sous le signe somme, donc 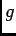 est de classe
est de classe
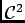 , avec:
, avec:
![\begin{displaymath}
\begin{array}[t]{ll}
g''(x)&=\ds\sum_{n= 1}^{+\infty}\dfra...
...infty}\dfrac{b_n\sin (nx)}{n^2+1}\\
&-f(x)+g(x)
\end{array}\end{displaymath}](img112.png)
et donc 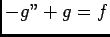 .
.
- La solution générale est de la forme
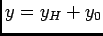 où
où 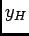 solution générale de l'équation sans second membre
solution générale de l'équation sans second membre 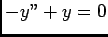 , alors
, alors
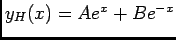 et
et 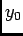 solution particulière avec second membre
solution particulière avec second membre 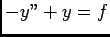 , d'aprés la question précédente
, d'aprés la question précédente 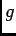 en est une, donc on peut prendre
en est une, donc on peut prendre 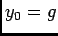 , d'où
, d'où
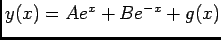 , or
, or
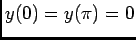 et
et
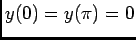 , d'où
, d'où 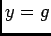 .
.
B- Cas où la suite
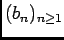 des coéfficients est décroissante.
des coéfficients est décroissante.
-
![\begin{displaymath}\begin{array}[t]{ll}
A_n(x)+iB_n(x)&=\ds\sum_{k= 1}^{n}\cos ...
...n }e^{ix}\\
&=\dfrac{1-e^{inx}}{1-e^{ix}}e^{ix}
\end{array}\end{displaymath}](img125.png) .
.
D'autre part en utilisant la relation
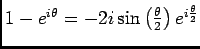 , on a:
, on a:
![\begin{displaymath}\begin{array}[t]{ll}
A_n(x)+iB_n(x)&=\dfrac{1-e^{inx}}{1-e^{...
...2\right)+i \sin \left( (n+1)\frac x2\right)\right)
\end{array}\end{displaymath}](img127.png) .
.
D'où
![\begin{displaymath}
\begin{array}[t]{l}B_n(x)=\dfrac{\sin\left(\frac{nx} 2\righ...
...(\frac x 2\right)}\cos \left( (n+1)\frac x2\right)
\end{array}\end{displaymath}](img128.png) ,
,
donc
![\begin{displaymath}\begin{array}[t]{ll}
\dfrac 12+A_n(x)&=\dfrac{2\sin\left(\fr...
...n+\frac 12) x\right)}{2\sin\left(\frac x 2\right)}
\end{array}\end{displaymath}](img129.png)
En utilisant la formule
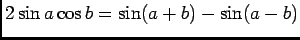 .
.
- Il faut ajouter dans la question ceci:
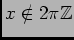 , dans ce cas
, dans ce cas
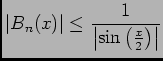 nombre réel qui ne dépond pas de
nombre réel qui ne dépond pas de 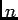 .
.
-
![\begin{displaymath}\begin{array}[t]{ll}
\ds\sum_{k= 1}^{n}b_k\sin (kx)&=\ds\sum...
..._k-b_{k+1})B_k(x)+b_nB_n(x)\qquad\text{ car }B_0=0
\end{array}\end{displaymath}](img134.png)
-
![\begin{displaymath}\begin{array}[t]{ll}
\ds\sum_{p= 1}^{n-1}\left\vert(b_p-b_{p...
...eft\vert \sin\left(\frac x 2\right)\right\vert}b_0
\end{array}\end{displaymath}](img135.png)
D'où la convergence absolue.
- D'aprés 2.1
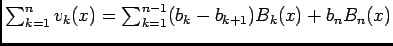 , avec
, avec
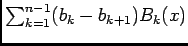 qui converge absolument,
qui converge absolument,
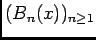 qui est bornée et
qui est bornée et
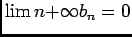 , d'où
, d'où
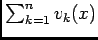 converge simplement dont la somme est impaire et
converge simplement dont la somme est impaire et 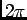 -périodique, en tant que limite simple de fonctions impaires et
-périodique, en tant que limite simple de fonctions impaires et 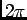 -périodiques.
-périodiques.
- Un exemple.
- D'aprés la question III.B.1.1 on a:
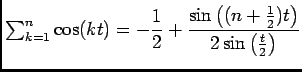 , on integre cette inégalité entre
, on integre cette inégalité entre 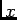 et
et 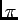 et on obtient:
et on obtient:
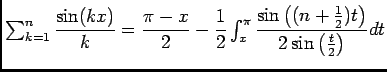
- Ca découle d'un résultat classique dont l'énoncé est le suivant:
Si 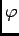 est de classe
est de classe
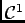 sur
sur ![$ [a,b]$](img143.png) , alors
, alors
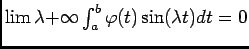
En effet, en posant
![\begin{displaymath}\begin{array}[t]{ll}
u'=sin(\lambda t)dt&\quad u=-\dfrac{cos...
...lambda}\\
v=\varphi(t)&\quad v'=\varphi'(t)\\
\end{array}\end{displaymath}](img145.png) ,
,
![$ M_0(\varphi)=\sup\limits_{[a,b]}\left\vert\varphi(t)\right\vert$](img146.png) et
et
![$ M_1(\varphi)=\sup\limits_{[a,b]}\left\vert\varphi'(t)\right\vert$](img147.png) On aura:
On aura:
![\begin{displaymath}\begin{array}[t]{ll}\left\vert\ds\int_a^b\varphi(t)\sin(\lamb...
...\
&\text{ quand }\lambda\longrightarrow +\infty
\end{array}\end{displaymath}](img148.png)
Et donc
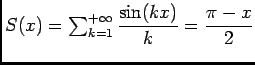 .
.
-
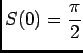 , ainsi
, ainsi 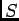 est discontinue en 0, car
est discontinue en 0, car
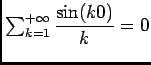 .
.
- Une condition nécessaire de continuité.
-
![\begin{displaymath}\begin{array}[t]{lll}
G(-\theta)&=\ds\int_0^{-\theta}f(t)dt&...
...eta}f(u)du&f\text{ est impaire.}\\
&=G(\theta)&
\end{array}\end{displaymath}](img153.png) .
.
D'autre part:
![\begin{displaymath}\begin{array}[t]{lll}
G(\theta+2\pi)&=\ds\int_0^{\theta+2\pi...
...nt_0^{2\pi}\sin(nu)du+G(\theta)&\\
&=G(\theta)&
\end{array}\end{displaymath}](img154.png)
- Dans cette question il s'agit d'un développement limité à l'ordre 1 au voisinage de 0, comme
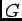 est de classe
est de classe
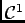 , en tant que primitive d'une fonction continue, alors ce développement est
, en tant que primitive d'une fonction continue, alors ce développement est
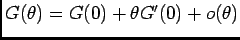 , or
, or 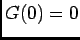 et
et
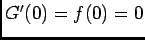 car
car 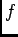 impaire. donc
impaire. donc
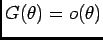 .
.
-
![\begin{displaymath}\begin{array}[t]{ll}
a_n(G)&=\dfrac 1\pi\ds\int_{-\pi}^{\pi}...
..._{-\pi}^{\pi}f(u)\sin(nt)du\\
&=-\dfrac {b_n}n
\end{array}\end{displaymath}](img159.png) .
.
D'autre part
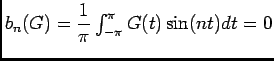 car
car
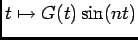 est impaire puisque
est impaire puisque 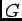 paire.
paire.
- Ainsi la série de Fourier associée à
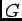 est
est
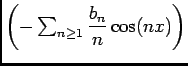 , elle converge simplement vers
, elle converge simplement vers
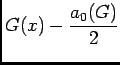 , puisque
, puisque 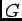 est de classe
est de classe
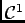 , ici il faut faire attention le
, ici il faut faire attention le 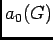 définie dans l'énoncé n'est pas le coéfficient de Fourier pour
définie dans l'énoncé n'est pas le coéfficient de Fourier pour 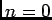 car ce dernier est donné par la formule
car ce dernier est donné par la formule
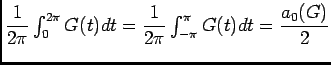 , puisque
, puisque 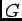 est paire.
est paire.
Pour 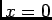 la série
la série
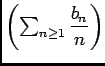 est convergente dont la somme est
est convergente dont la somme est
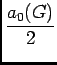 .
.
- On a:
![\begin{displaymath}\begin{array}[t]{lll}
E\left(\dfrac k2\right)&=\dfrac k2&\te...
...}\\
&=\dfrac {k-1}2&\text{si }k\text{ impair}
\end{array}\end{displaymath}](img170.png) .
.
Dans tous les cas:
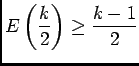 , si
, si
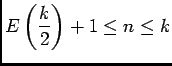 , alors
, alors
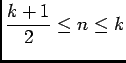 , donc
, donc
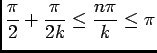 , et alors
, et alors
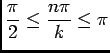 , donc
, donc
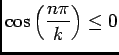 . Et donc
. Et donc
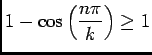 , d'où
, d'où
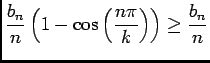 , or
, or
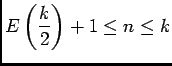 , donc
, donc
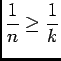 et
et 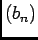 est décroissante, donc
est décroissante, donc
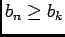 , d'où
, d'où
![\begin{displaymath}
\begin{array}[t]{ll}
\ds\sum_{n=E\left(\frac k2\right)+1}^...
...\right)\right)\dfrac{b_k}k\\
&\soe \dfrac{b_k}2
\end{array}\end{displaymath}](img181.png)
car 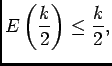 donc
donc 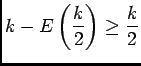
-
![\begin{displaymath}\begin{array}[t]{ll}
G\left(\dfrac\pi k\right)&=\dfrac{a_0(G...
...b_n}n\left(1-\cos\left(\dfrac{n\pi}k\right)\right)
\end{array}\end{displaymath}](img184.png)
Ainsi
![\begin{displaymath}\begin{array}[t]{ll}
G\left(\dfrac\pi k\right)&=\ds\sum_{n= ...
...dfrac{n\pi}k\right)\right)\\
&\soe \dfrac{b_k}2
\end{array}\end{displaymath}](img185.png)
Et donc
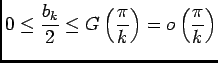 , d'où
, d'où
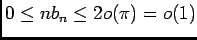 , donc
, donc
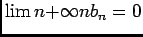 .
.
Fin du corrigé.



suivant: À propos de ce
root
2006-02-26
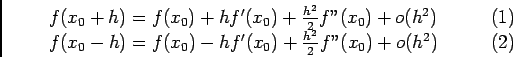
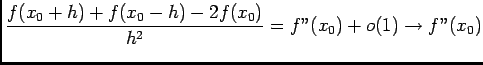 , quand
, quand
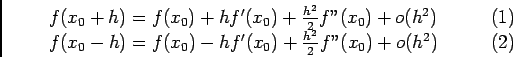
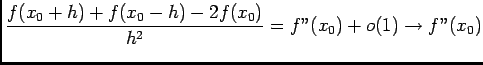 , quand
, quand
![\begin{displaymath}\begin{array}{ll}
\\ ds\int_0^{2\pi}b_n^2\sin^2(nx)dx&=\dfr...
...n(2nx)}{2n}\right]_{x=0}^{x=2\pi}\\
&=\pi b_n^2
\end{array}\end{displaymath}](img7.png) .
.
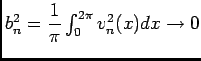 , quand
, quand
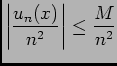 et d'autre part
et d'autre part
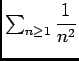 est une série de Riemann convergente, donc
est une série de Riemann convergente, donc
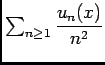 converge normalement, dont le terme général est continue donc sa somme est aussi continue.
converge normalement, dont le terme général est continue donc sa somme est aussi continue.
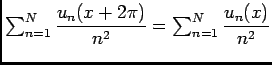 , quand on fait tendre
, quand on fait tendre 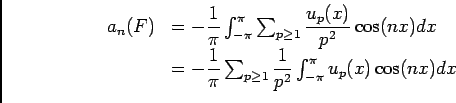
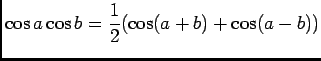 , donc
, donc
![$ \ds\int_{-\pi}^\pi\cos(px)\cos(nx)dx=\dfrac 12\ds\int_{-\pi}^\pi(\cos (n+p)x+\...
...eft[\dfrac{\sin (n+p)x}{n+p}+\dfrac{\sin (n-p)x}{n-p}\right]_{x=-\pi}^{x=\pi}=0$](img48.png) si
si ![$ \ds\int_{-\pi}^\pi\cos(px)\cos(nx)dx=\ds\int_{-\pi}^\pi\cos^2(nx)dx=\dfrac 12\...
...+p)x+1)dx=\dfrac 12\left[\dfrac{\sin (n+p)x}{n+p}+x\right]_{x=-\pi}^{x=\pi}=\pi$](img51.png) .
.
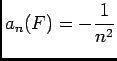 . Et pareil pour le calcul de
. Et pareil pour le calcul de 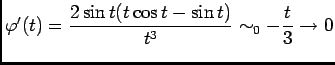 quand
quand
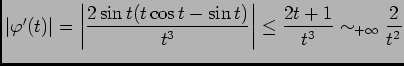 , intégrable au voisinage de
, intégrable au voisinage de ![\begin{displaymath}\begin{array}[t]{l}
\dfrac{F(x+2h)+F(x-2h)-2F(x)}{4h^2}\\ ...
...}^{+\infty}(a_n\cos (nx)+b_n\sin (nx))\varphi (nh)
\end{array}\end{displaymath}](img63.png)
![\begin{displaymath}\begin{array}[t]{l}
\ds\sum_{n=0}^{+\infty}\left(S_n(x)-f(x)...
...nx)\\
=\dfrac{F(x+2h)+F(x-2h)-2F(x)}{4h^2}-f(x)
\end{array}\end{displaymath}](img64.png)
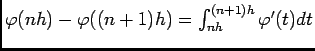 , donc
, donc
![\begin{displaymath}\begin{array}[t]{l}
\left\vert\ds\sum_{n=N}^{+\infty}\left(S...
...0}^{+\infty}\left\vert\varphi '(t)\right\vert dt=A
\end{array}\end{displaymath}](img67.png)
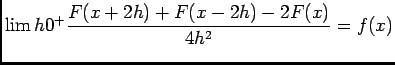
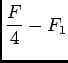 est affine au lieu de
est affine au lieu de ![\begin{displaymath}\begin{array}[t]{ll}
u'(t)=f(t)&\quad u=G(t)\\
v(t)=x-t&\quad v'(t)=-1
\end{array}
\end{displaymath}](img78.png) , alors
, alors
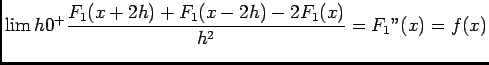 , on pose
, on pose
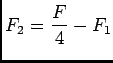 , alors:
, alors:
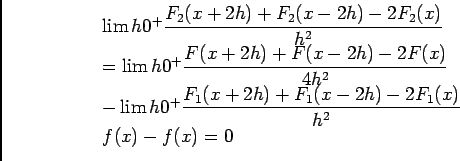
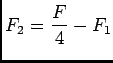 est affine et par suite
est affine et par suite 
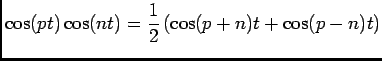 , donc:
, donc:
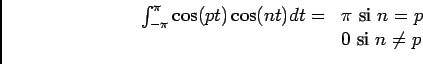
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v_n(x)}{n^2(n^2+1)}\ri...
...oe \dfrac{M}{n^2(n^2+1)}\\
&\ioe \dfrac{M}{n^4}
\end{array}\end{displaymath}](img97.png) et
et
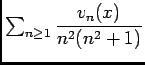 converge normalement sur
converge normalement sur
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v'_n(x)}{n^2(n^2+1)}\r...
...\ioe \dfrac{M}{n(n^2+1)}\\
&\ioe \dfrac{M}{n^3}
\end{array}\end{displaymath}](img100.png) et
et
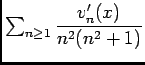 converge normalement sur
converge normalement sur
![\begin{displaymath}\begin{array}[t]{ll}
\left\vert\dfrac{v''_n(x)}{n^2(n^2+1)}\...
...&\ioe \dfrac{M}{(n^2+1)}\\
&\ioe \dfrac{M}{n^2}
\end{array}\end{displaymath}](img103.png) et
et
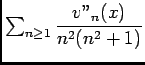 converge normalement sur
converge normalement sur
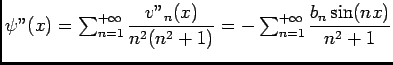 .
.
 converge simplement et continue, donc
converge simplement et continue, donc
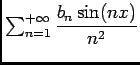 est de classe
est de classe
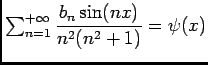 , avec la possibilité de dériver sous le signe somme, donc
, avec la possibilité de dériver sous le signe somme, donc ![\begin{displaymath}
\begin{array}[t]{ll}
g''(x)&=\ds\sum_{n= 1}^{+\infty}\dfra...
...infty}\dfrac{b_n\sin (nx)}{n^2+1}\\
&-f(x)+g(x)
\end{array}\end{displaymath}](img112.png)
![\begin{displaymath}\begin{array}[t]{ll}
A_n(x)+iB_n(x)&=\ds\sum_{k= 1}^{n}\cos ...
...n }e^{ix}\\
&=\dfrac{1-e^{inx}}{1-e^{ix}}e^{ix}
\end{array}\end{displaymath}](img125.png) .
.
![\begin{displaymath}\begin{array}[t]{ll}
A_n(x)+iB_n(x)&=\dfrac{1-e^{inx}}{1-e^{...
...2\right)+i \sin \left( (n+1)\frac x2\right)\right)
\end{array}\end{displaymath}](img127.png) .
.
![\begin{displaymath}
\begin{array}[t]{l}B_n(x)=\dfrac{\sin\left(\frac{nx} 2\righ...
...(\frac x 2\right)}\cos \left( (n+1)\frac x2\right)
\end{array}\end{displaymath}](img128.png) ,
,
![\begin{displaymath}\begin{array}[t]{ll}
\dfrac 12+A_n(x)&=\dfrac{2\sin\left(\fr...
...n+\frac 12) x\right)}{2\sin\left(\frac x 2\right)}
\end{array}\end{displaymath}](img129.png)
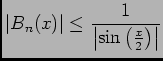 nombre réel qui ne dépond pas de
nombre réel qui ne dépond pas de ![\begin{displaymath}\begin{array}[t]{ll}
\ds\sum_{k= 1}^{n}b_k\sin (kx)&=\ds\sum...
..._k-b_{k+1})B_k(x)+b_nB_n(x)\qquad\text{ car }B_0=0
\end{array}\end{displaymath}](img134.png)
![\begin{displaymath}\begin{array}[t]{ll}
\ds\sum_{p= 1}^{n-1}\left\vert(b_p-b_{p...
...eft\vert \sin\left(\frac x 2\right)\right\vert}b_0
\end{array}\end{displaymath}](img135.png)
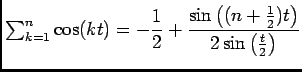 , on integre cette inégalité entre
, on integre cette inégalité entre 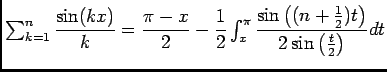
![\begin{displaymath}\begin{array}[t]{ll}
u'=sin(\lambda t)dt&\quad u=-\dfrac{cos...
...lambda}\\
v=\varphi(t)&\quad v'=\varphi'(t)\\
\end{array}\end{displaymath}](img145.png) ,
,
![$ M_0(\varphi)=\sup\limits_{[a,b]}\left\vert\varphi(t)\right\vert$](img146.png) et
et
![$ M_1(\varphi)=\sup\limits_{[a,b]}\left\vert\varphi'(t)\right\vert$](img147.png) On aura:
On aura:
![\begin{displaymath}\begin{array}[t]{ll}\left\vert\ds\int_a^b\varphi(t)\sin(\lamb...
...\
&\text{ quand }\lambda\longrightarrow +\infty
\end{array}\end{displaymath}](img148.png)
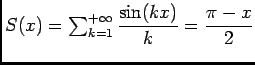 .
.
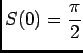 , ainsi
, ainsi 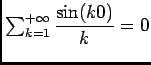 .
.
![\begin{displaymath}\begin{array}[t]{lll}
G(-\theta)&=\ds\int_0^{-\theta}f(t)dt&...
...eta}f(u)du&f\text{ est impaire.}\\
&=G(\theta)&
\end{array}\end{displaymath}](img153.png) .
.
![\begin{displaymath}\begin{array}[t]{lll}
G(\theta+2\pi)&=\ds\int_0^{\theta+2\pi...
...nt_0^{2\pi}\sin(nu)du+G(\theta)&\\
&=G(\theta)&
\end{array}\end{displaymath}](img154.png)
![\begin{displaymath}\begin{array}[t]{ll}
a_n(G)&=\dfrac 1\pi\ds\int_{-\pi}^{\pi}...
..._{-\pi}^{\pi}f(u)\sin(nt)du\\
&=-\dfrac {b_n}n
\end{array}\end{displaymath}](img159.png) .
.
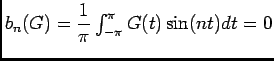 car
car
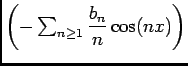 , elle converge simplement vers
, elle converge simplement vers
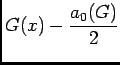 , puisque
, puisque 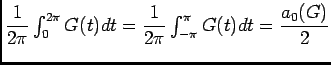 , puisque
, puisque 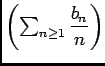 est convergente dont la somme est
est convergente dont la somme est
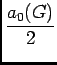 .
.
![\begin{displaymath}\begin{array}[t]{lll}
E\left(\dfrac k2\right)&=\dfrac k2&\te...
...}\\
&=\dfrac {k-1}2&\text{si }k\text{ impair}
\end{array}\end{displaymath}](img170.png) .
.
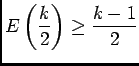 , si
, si
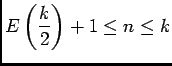 , alors
, alors
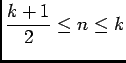 , donc
, donc
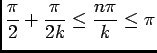 , et alors
, et alors
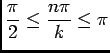 , donc
, donc
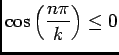 . Et donc
. Et donc
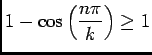 , d'où
, d'où
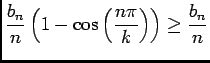 , or
, or
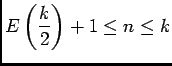 , donc
, donc
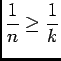 et
et ![\begin{displaymath}
\begin{array}[t]{ll}
\ds\sum_{n=E\left(\frac k2\right)+1}^...
...\right)\right)\dfrac{b_k}k\\
&\soe \dfrac{b_k}2
\end{array}\end{displaymath}](img181.png)
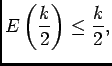 donc
donc 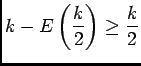
![\begin{displaymath}\begin{array}[t]{ll}
G\left(\dfrac\pi k\right)&=\dfrac{a_0(G...
...b_n}n\left(1-\cos\left(\dfrac{n\pi}k\right)\right)
\end{array}\end{displaymath}](img184.png)
![\begin{displaymath}\begin{array}[t]{ll}
G\left(\dfrac\pi k\right)&=\ds\sum_{n= ...
...dfrac{n\pi}k\right)\right)\\
&\soe \dfrac{b_k}2
\end{array}\end{displaymath}](img185.png)
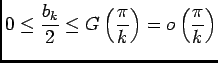 , d'où
, d'où