- On a
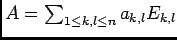 , donc:
, donc:
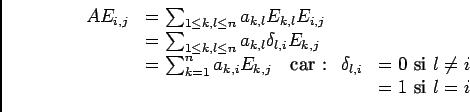
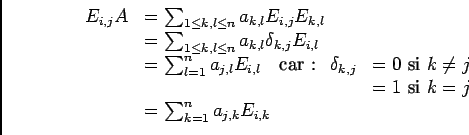
-
![\begin{displaymath}\begin{array}[t]{ll}
AM=MA&\;\Longrightarrow\;AM-MA=0\\
&\;...
...i}E_{k,j}-a_{j,k}E_{i,k}+(a_{i,i}-a_{j,j})E_{i,j}=0
\end{array}\end{displaymath}](img5.png)
Ainsi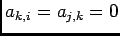 si
si 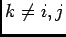 et
et
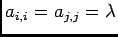 , d'où
, d'où
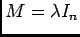
- On sait que la trace est linéaire et que:
![\begin{displaymath}\begin{array}[t]{ll}Tr(E_{k,j})&=0\text{ si }k\neq j\\ &=1\text{ si }k= j\end{array}\end{displaymath}](img10.png) , donc
, donc
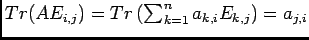 .
.
-
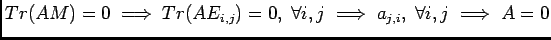 .
.
| Corrigé Concours marocain, 2006 |
| Math II, MP |
|---|
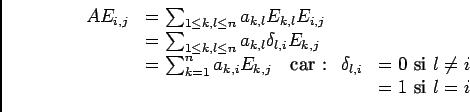
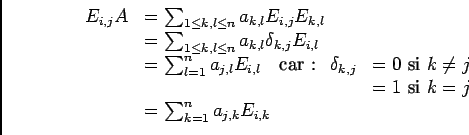
![\begin{displaymath}\begin{array}[t]{ll}
AM=MA&\;\Longrightarrow\;AM-MA=0\\
&\;...
...i}E_{k,j}-a_{j,k}E_{i,k}+(a_{i,i}-a_{j,j})E_{i,j}=0
\end{array}\end{displaymath}](img5.png)
![\begin{displaymath}\begin{array}[t]{ll}Tr(E_{k,j})&=0\text{ si }k\neq j\\ &=1\text{ si }k= j\end{array}\end{displaymath}](img10.png) , donc
, donc
![\begin{displaymath}
\begin{array}[t]{ll}
&Tr\left((\Phi(A+B)-\Phi(A)-\Phi(B))\Ph...
...ace est linéaire et . distributive par rapport à +}
\end{array}\end{displaymath}](img84.png)
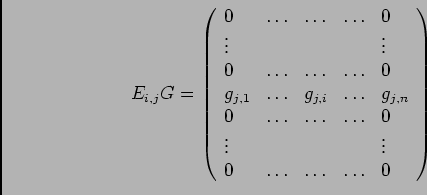 , donc sont polynôme caractéristique est
, donc sont polynôme caractéristique est
![\begin{displaymath}\begin{array}[t]{ll}
A\text{ positive }&\ssi ^tXAX\soe 0\;\ql...
...ext{Toutes les valeurs propres de A sont positives}
\end{array}\end{displaymath}](img142.png)
![\begin{displaymath}\begin{array}[t]{ll}
\lambda\in\text{Sp}_\ensuremath{\mathbb{...
...\lambda\in\text{Sp}_\ensuremath{\mathbb{R}} (A)+\mu
\end{array}\end{displaymath}](img143.png)
![\begin{displaymath}\begin{array}[t]{ll}
A+xI_n\text{ définie positive }&\ssi \te...
...t{Sp}_\ensuremath{\mathbb{R}} (A)),\;\qlq x >\alpha
\end{array}\end{displaymath}](img146.png)
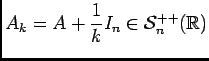 , car ses valeurs propres,
, car ses valeurs propres,
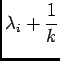 sont strictement positives, de plus
sont strictement positives, de plus